|
This is the school book-club book and it is simply wonderful. You should read it!! Our meeting is on April 13. I can lend you the book if you want it.
This week's Student of the Week is William A!
I am so happy that William is nearing the end of Pre-Calculus 12. Not because I want to see him leave (I don't! I don't!) but because I know that Math has - at times - been quite difficult for William. Mind you, part of the reason is William's own fault (more on that later), but still... I am pleased that he is going to successfully complete PreCalc 12 (if you KEEP ON WORKING WILLIAM!!!). I can't NOT say it... the number one thing I associate with William is him BEING LATE ALMOST EVERY SINGLE CLASS!! It's really quite amazing (almost impressive even). It's been this way right from grade 10 when I first taught him. William would slink into class (wordlessly, and maybe a bit sheepishly) between 15 and 40 minutes late. It got to the point where I told him once: "just be here within the first 10 minutes and I will still count you as on-time". I don't think that worked even a little bit. Of course, there has been the odd time when William is on time. It's always great fun to make a huge deal about it, pretend I don't recognize him, ask how it got so late in class, etc. It never ceases to amuse me (even if William doesn't look all that impressed. Sorry W.A.!). Often students who come late all the time have a bit of an attitude. Kind of like: "school sucks so I'll come when I want and what can you do about it anyway..?". William is not like this at all. He has never had the slightest bit of attitude with me. He has always been polite and appreciative. He is a kind and soft-spoken student... and a good guy! And it's not surprising because (hope this doesn't embarrass you William) William has such a nice mom!! I ALWAYS look forward to seeing her at parent-teacher conferences. She is so vibrant and happy and supportive of William. Plus, she always says kind things to me (and gets me Christmas presents!). What a lovely lady! What a lovely family! Thanks to you both! William, I am really proud of you for "sticking with Math" over the years. It would have been easy to say "this isn't for me" and stopped in grade 11 but you have pushed on and you will (you BETTER!!!) pass PreCalc 12 this year! Thanks for being such a good sport and a nice person. I wish you all the best in the years ahead!! As I may have told you, we lucked into First Class Tickets on our way to and from Mexico. So here is how we all spent the time home yesterday... Sophia read a book (for school book club no less!). It makes me so happy when she reads books (and not her phone). hehehe My mother-in-law felt sick and went with this look. And, no, she is not just posing / joking. This was a "choice". Zan looking "disappointed" (or is that look known as IRATE) for how cold it was in the plane (in first class, no less!!). This dork worked on Sudoku and Ken-Ken puzzles the whole way. Nice posture Buddy! This kid has got first class figured out.
Glad he finally got this award. The story of him solving Fermat's Last Theorem is pretty amazing!20/3/2016 One of the main intuitive ideas about the distribution of the primes that mathematicians have traditionally held is that they are distributed somewhat "randomly." That is, there aren't particular patterns to be found in the prime numbers.
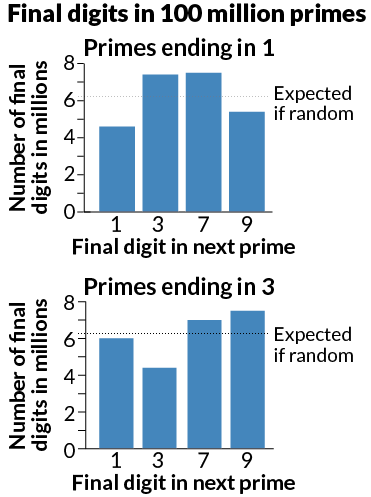
However Professor Kannan Soundararajan and Dr Robert Lemke Oliver from Stanford University believe they have found such a pattern. The pair said they had uncovered that primes, which end in a particular digit, were less likely to be followed by another prime which also ends in that digit. Prime numbers larger than 5 have to end in a 1, 3, 7, or 9: Numbers that end with an even digit are divisible by 2 and therefore not prime, and numbers with a final digit of 5 are divisible by 5. Under the idea that the primes are randomly distributed, then, the odds of a prime ending in 1 being followed by another prime ending in 1 would be 25%: Final digits should be evenly distributed among the four possibilities mentioned above. But Soundararajan and Oliver’s research showed the actual odds were closer to 18%. A prime ending in 1 actually has a greatly increased chance of being followed by a figure ending in 3 or 7 (around 30%) and a 22% chance of the figure ending with a 9. That non-random behavior is very surprising and challenges mathematicians' assumptions about prime numbers. Number theorist Andrew Granville: "We’ve been studying primes for a long time, and no one spotted this before. It’s crazy." |
P. WadgeI am your teacher. Obey me. Archives
June 2021
Categories
All
|











 RSS Feed
RSS Feed