However Professor Kannan Soundararajan and Dr Robert Lemke Oliver from Stanford University believe they have found such a pattern.
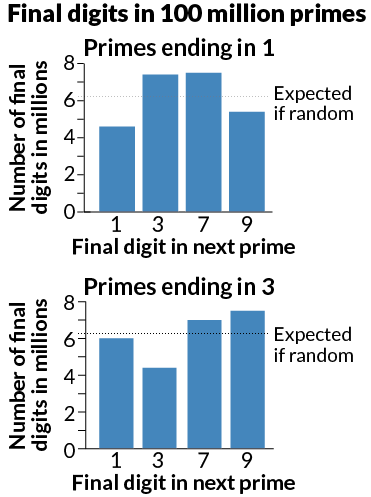
The pair said they had uncovered that primes, which end in a particular digit, were less likely to be followed by another prime which also ends in that digit. Prime numbers larger than 5 have to end in a 1, 3, 7, or 9: Numbers that end with an even digit are divisible by 2 and therefore not prime, and numbers with a final digit of 5 are divisible by 5.
Under the idea that the primes are randomly distributed, then, the odds of a prime ending in 1 being followed by another prime ending in 1 would be 25%: Final digits should be evenly distributed among the four possibilities mentioned above.
But Soundararajan and Oliver’s research showed the actual odds were closer to 18%.
A prime ending in 1 actually has a greatly increased chance of being followed by a figure ending in 3 or 7 (around 30%) and a 22% chance of the figure ending with a 9.
That non-random behavior is very surprising and challenges mathematicians' assumptions about prime numbers. Number theorist Andrew Granville: "We’ve been studying primes for a long time, and no one spotted this before. It’s crazy."
 RSS Feed
RSS Feed